Appended Note 3-6 Characteristics of Various Inequality Indexes
- Japanese version
- English version
1. Atkinson index (AI)
This is an indicator calculated by taking account of the degree to which income disparity is tolerated. First, on the basis of the income distribution that exists, calculate the degree of obtainable social welfare (the degree of happiness of the overall society) from it. Then, in order to reproduce that social welfare, calculate backward how much income can be distributed to people in an equal way. That income is referred to as "equally distributed income." The Atkinson coefficient is a value indicated with a ratio the degree to which the equally distributed income falls below the actually measured average income. It is relatively sensitive to the changes of the two extremes of income distribution.
The formula is shown as follows. In this analysis, the index was calculated with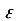 
= 0.5.
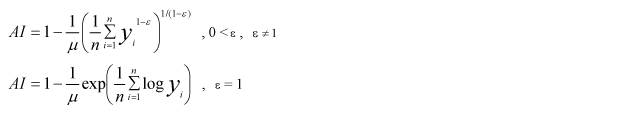
2. Mean Logarithm Deviation (MLD)
The MLD is derived by calculating the logarithmical value of the ratio of each individual's income to the average income to find the average for that society as a whole. The value of this MLD is zero if income is distributed in a perfectly equal way and becomes larger if the degree of inequality rises. It is relatively sensitive to change in the income distribution among low-income groups.
The formula is shown as follows:
3. Tile index (TI)
The TI is derived by taking the difference between the logarithm of the average income and the logarithm of each individual's income and calculating the weighted average by using the weight of each individual's income. The index is zero if income is distributed in a perfectly equal way and becomes larger if the degree of inequality rises. It is relatively sensitive to change in the income distribution among low-income groups.
The formula is shown as follows:
(where yi stands for income of household No.i,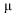 
for its average and n for the number of households)
Note: 1. Reference: "Social Security Reforms in an Era with Dwindling Population" (by T. Oshio, 2005) and "Economics for Social Security" (by T. Oshio, 1998)