付注1－1　ランダムフォレストとベイジアン・ネットワーク

＜ランダムフォレスト＞

ランダムフォレストは、ブートストラップ法により、データからランダムにサンプリングされた訓練データをもとに、多くの決定木を作成し、それらをまとめることで推計値を得る手法である。

ただし、本分析の目的は推計値を得ることでなく、被説明変数（消費者マインド）に対し、各説明変数（消費者物価指数や株価等）の与える影響度合いが高いものを見つけることであるため、今回は変数重要度と呼ばれる指標を用いて、各変数の影響を評価した。

変数重要度は、説明変数ごとに観測値をランダムに並び替えた場合、予測誤差がどの程度大きくなるかを計測したもので、予測誤差の大きい説明変数ほど重要度が高いと評価できる。なお、具体的には、観測値の約3分の2のデータを用いて学習を行い、残り3分の1のデータを用いて、変数重要度の計算を行う。

＜ベイジアン・ネットワーク＞

ランダムフォレストは、消費者マインドと関係のある変数を見つけるのには役に立つ手法であるが、変数間の因果関係について知ることはできない。例えば、消費者マインドと株価に何らかの関係が見られた場合、どちらが原因でどちらが結果なのか、ランダムフォレストからは判別ができない。

そこで、本分析では、ベイジアン・ネットワークと呼ばれる手法を用いて、消費者マインドと各説明変数の因果関係の識別を試みた。

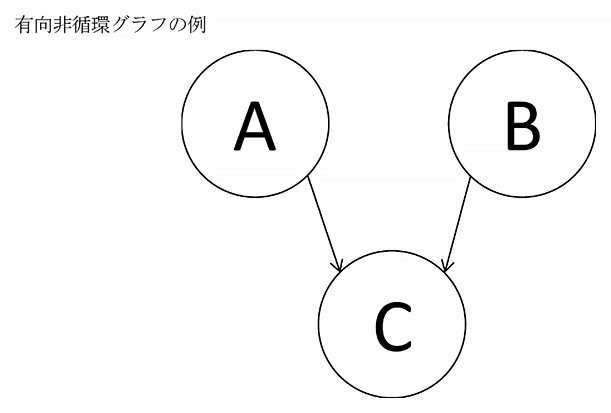
ベイジアン・ネットワークは、確率変数間の定量的な関係を条件付き確率で表現したうえで、定性的な依存関係を有向非循環グラフによって表すモデルである。例えば、確率変数AとBがそれぞれ確率変数Cに影響を与えるとすると、この関係は次ページの様に表現できる。各変数を表す丸をノード、ノードを結ぶ線をエッジと呼び、矢印の方向が因果を表している。また、エッジの矢印の向きを無視してグラフを見たものをスケルトンと言う。

本分析では、PCアルゴリズムと呼ばれる手法を用いて、こうした因果関係の推定を行う。PCアルゴリズムでは、確率変数間の条件付き独立を検定し、条件付き独立が認められれば、各確率変数は分離されているとみなす。例えば、確率変数AとBについて、仮にCを前提とすると、AとBの結びつきが弱くなるのであれば、AとBは直接は結びついていないとみなせる。こうした作業を全ての変数間で行い、因果関係を推定していく。