付注3－4　異時点間の平均対数偏差変化の要因分

所得分布の格差を把握する指数である平均対数偏差（以下、MLDという。）は、母集団の格差を、母集団を何らかのグループ別にわけたグループ内の格差とグループ間の格差に要因分解できる性質をもつ。例えば、母集団が全部でmのグループで構成され、第g階層の所得平均と平均対数偏差及び全体に占める比率をそれぞれYg, MLDg, αgとすると、

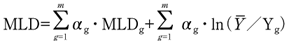
と表現することができる。

この性質を用いて、Mookherjee and Shorrocks（1982）に基づきMLDの変化について要因分解を行うと、時点0から時点1にかけてのMLDの変化ΔMLDは、

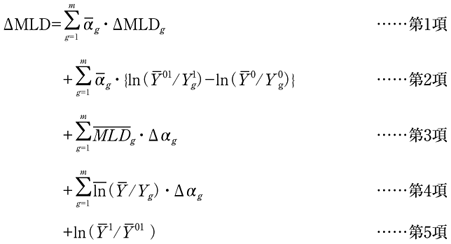
と表される。ここで、母集団をm年齢階層に区分したとして、

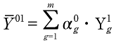
は、年齢構成を時点0で固定した上での時点1における第g年齢階層の平均所得を表し、式中のバーは、それぞれの値の時点0及び1における平均値を表すものとする。

この式における、

[1]右辺第1項は、同一年齢階層内部の格差変化による全体の所得格差変化の寄与度（年齢階層内効果）

[2]右辺第2項は、異なる年齢階層間の格差変化による全体の所得格差変化の寄与度（年齢階層間効果）

[3]残り3つの項の合計は、0時点における格差を固定したとして、人口構成が変化することによる全体の所得格差変化の寄与度（人口動態効果）

を意味している。