第2章 2024年前半の世界経済の動向(付注2-1)
付注2-1 マルコフ・スイッチングモデルによるドイツの景気循環の分析
1.データ出所
ドイツ連邦統計局の鉱工業生産指数(総合、季節調整値、1991年1月~2024年4月)、ドイツ経済諮問委員会が設定するドイツの景気基準日付を用いた。
2.推計方法
マルコフ・スイッチングモデルでは、景気後退期と景気拡張期の2つの状態が存在すると考え、この2つの状態がマルコフ連鎖にしたがい、時々スイッチすると考える。
時点t(t=1,…,T)における状態をStとし、状態が1(景気後退期)または2(景気拡張期)の2状態しかないモデルを考える。この時、Stの条件付確率関数が次のようなマルコフ連鎖にしたがうと仮定する。
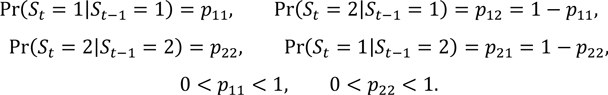
また、xtを鉱工業生産指数とし、鉱工業生産指数の前月比を以下のとおり対数階差の100倍として表す。
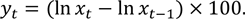
これらの仮定のもとで、モデル式を以下のとおり表す143。
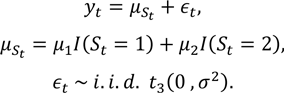
ただし、I(∙)は指示関数(Aが真の時I(A)=1、それ以外は0)。
ここで、確率密度関数をπ(∙)、尤度関数をf(∙)で表すと、ベイズの定理より、事後確率密度関数は以下のとおり表せる。
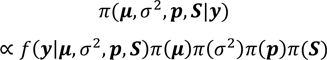
ただし、
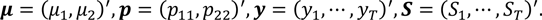
この事後確率密度関数の各パラメータを、マルコフ連鎖モンテカルロ法144を用いて推定を行った。各パラメータが推定できれば、求めたい景気後退の事後確率
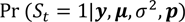
の確率分布を求めることができる。
なお、事前分布は、以下のとおり設定した145。
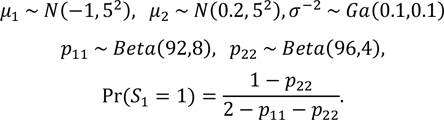
3.推計結果146

143 tν(μ,σ2)は、自由度ν、平均μ、分散σ2のt分布を表す。ϵtに正規分布を仮定した場合、コロナ禍で生産が大きく落ち込んだ時点のみが景気後退と認識され、他の景気循環を検出できない。裾が厚いt分布を用いることで、コロナ禍の時期が外れ値として認識される結果、他の景気循環を認識できる。なお、AICやBIC、確率標本の定常分布への収束度合いを勘案し、t分布の自由度は3とした。
144 マルコフ連鎖モンテカルロ(Markov chain Monte Carlo: MCMC)法とは、事後分布が定常分布になるようなマルコフ連鎖を構成することで、事後分布からの確率標本を得る手法のことである。今回の例のように事後分布が多次元であり、各パラメータに関する周辺事後確率密度関数を数値積分で求めることが困難な場合であっても、MCMC法によって事後分布からの確率標本を得ることで、事後分布に関する推論を行うことができる。MCMC法の実行にあたっては、確率的プログラミング言語Stanを用いた。MCMC法を実行する際、確率標本が定常分布に収束するまでは、初期値に依存する期間の確率標本を稼動検査期間(burn-in period)として捨て、それ以降の確率標本を用いて推論を行う。ここでは、最初の1,000個の確率標本を稼動検査期間として捨て、その後の10,000個の確率標本を推論に使用した。MCMC法の詳細については、大森他(2008)を参照のこと。
145 N(μ,σ2)は平均μ、分散σ2の正規分布、Ga(α,β)は形状母数(shape parameter)α、尺度母数(scale parameter)βのガンマ分布、Beta(α,β)はパラメータα、βのベータ分布を表す。ガンマ分布、ベータ分布の詳細については、久保川(2017)を参照のこと。σ(-2)は平均1、標準偏差3.2であり情報が少ない事前分布を仮定している。p11は平均0.92、標準偏差0.03、p22は平均0.96、標準偏差0.02と強めの事前分布を仮定しており、安定的に各景気循環が検出されるようにしている。なお、コロナ禍前の期間である1991年~2019年にドイツ経済諮問委員会が景気後退とみなした景気後退期の実績を用いて得られる推定値は、p̂11=∑tI(St=1,St-1=1)/∑tI(St-1=1)=0.95、p̂22=∑tI(St=2,St-1=2)/∑tI(St-1=2)=0.99である。本分析では(実際には景気後退と認定されていない)2023年3月以降において景気後退期への局面変化の可能性がどの程度高まっていたのかが関心の対象であることから、実際に景気後退と認定された時期よりも広く景気後退が検出されるように、事前分布の平均値を低く設定している。
146 「事後平均」はパラメータの事後分布の平均値、「事後標準偏差」はパラメータの事後分布の標準偏差、「95%信用区間」は95%の確率でパラメータが入る区間、「有効標本数」はMCMC法によって得た確率標本の精度が独立な標本いくつ分に相当するかを表す(大森他(2008))。

