付注2-1 ランダムフォレスト・決定木分類について
本分析には機械学習(machine learning)の分野で広く知られているランダムフォレスト(random forest)と呼ばれる手法を用い、「機械」が学習した結果を通じて説明変数の影響度合いを推定する。ランダムフォレストは特定の関数式を仮定しないため、従来の回帰モデルとは異なり説明変数の選択に制約が非常に少なく、過学習(over-fitting)の影響を排し多くの変数を説明変数として用いることが可能である。これは、ランダムフォレストが過学習を回避するため、ひとつのデータをリサンプリングして複数の回帰木(regression tree)を学習するためである。この回帰木のサンプルを分割するたびに、全ての説明変数からランダムにいくつかの説明変数を選ぶことからランダムフォレストと呼ばれている。尚、本分析では、N個の説明変数からランダムに√N個の説明変数を選んで学習させている。
分析の目的は説明変数が被説明変数に対し、どの程度影響するかを探索することであるため、ランダムフォレストの予測値ではなく、変数重要度(variable importance)を用いて影響を評価した。ランダムフォレストは従来の回帰モデルのように説明変数の係数を推定するわけではないため、説明変数がランダムで選択された際の予測誤差の大きさを計測した変数重要度が一般的に評価では用いられる。予測誤差が大きいほど変数への重要度が高いと評価できるため、変数重要度の高い説明変数ほど被説明変数への影響度が高いと考える。
また、第2-3-7図では、職業設計を労働者自身で検討したいとの割合が高いセグメントを探索するため、決定木学習(decision tree learning)も併せて行った。決定木による分類は、説明変数によるサンプルの分割を繰り返しながら徐々に分類目的(職業設計を自分で実施)の予測誤差を小さくしていく手法である。説明変数間の相互作用を考慮した分類が可能であり、複数の説明変数で分割していくことで職業設計を自分でしたい人の比率が高まる(低まる)樹形図(tree)が作成できる。
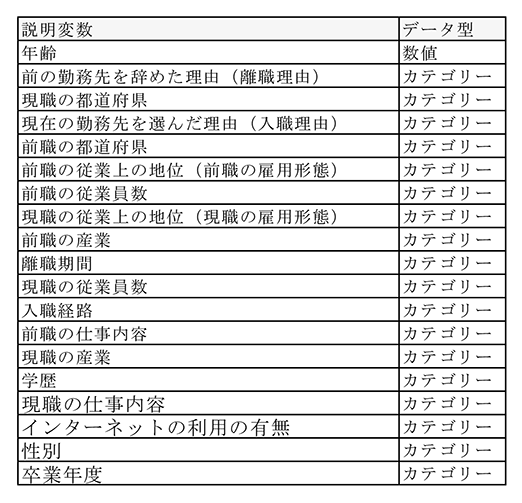
2 第2-1-7図について厚生労働省「雇用動向調査」の2006年、2016年の個票データを用いて分析を行った。被説明変数は、転職後の賃金変動(7カテゴリー)である。説明変数については、付注2-1表1の通りであるが、現職の産業については、大分類ベースで集計を行った。また、インターネット利用に関しては、簡素化のため、利用状況に関わらず、利用したか否かで2種類の分類変数に変換している。なお、産業分類・職業分類については、分類の改定により2016年と2006年とで分類が異なる。
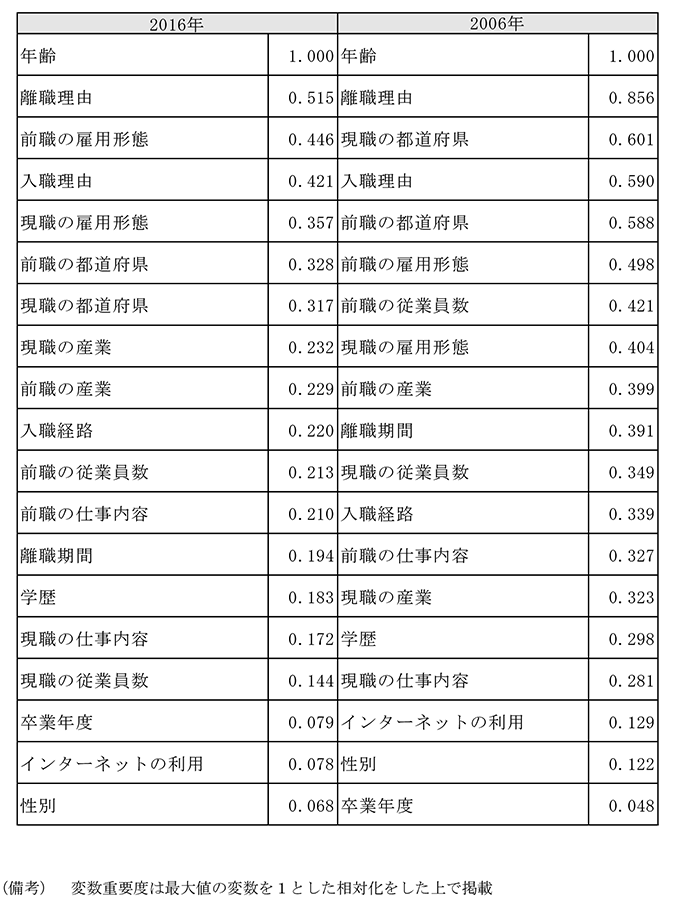
ランダムフォレストの分析結果は付注2-1表2の通りである。
3 第2-3-7図について(データ)
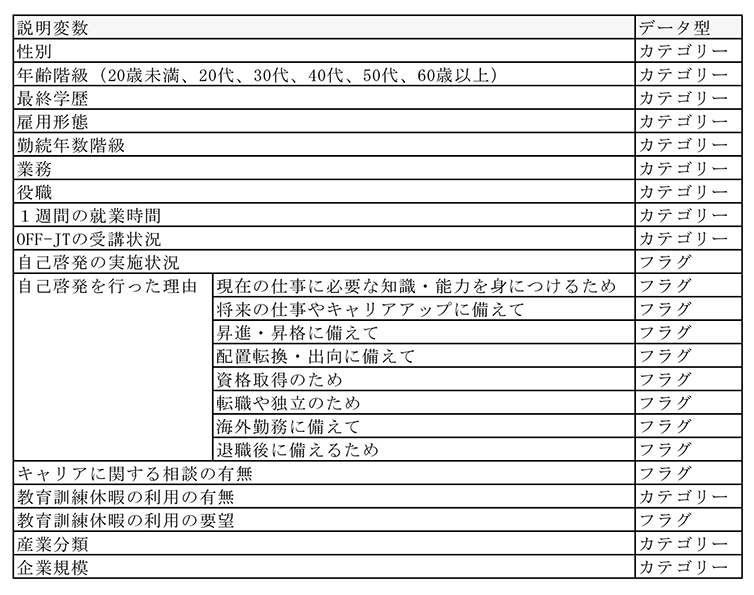
厚生労働省「平成28年度 能力開発基本調査」の個票データを用い、正社員・正社員以外について、別々に分析を実施した。被説明変数は「職業生活設計の考え方」という問いに対し、「自分で職業生活設計を考えていきたい」若しくは「どちらかといえば、自分で職業生活設計を考えていきたい」を回答した労働者を「自分で職業設計をしたい人」と定義し、分類変数として作成した。説明変数は付注2-1表3の通り23変数を用いた。
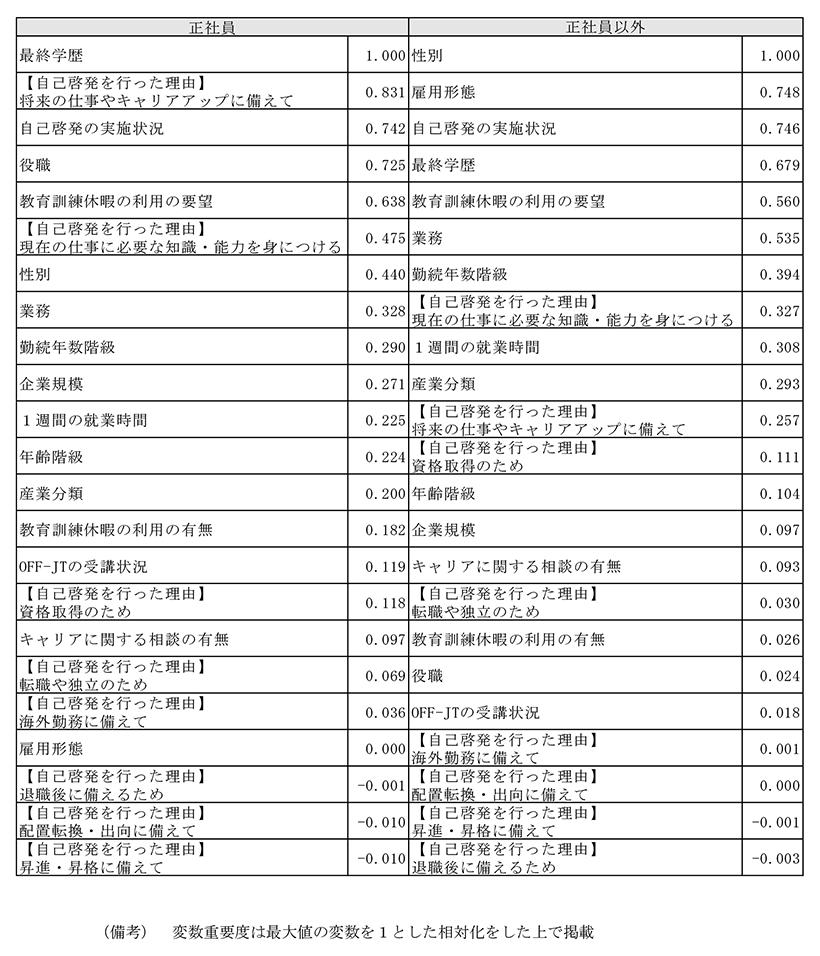
(ランダムフォレストの分析結果について(補足))ランダムフォレストの分析結果は付注2-1表4の通りである。
正社員・正社員以外で共通した傾向として「自己啓発の実施」が大きく影響している。職業設計を自発的にしたい労働者は将来に備える目的で自己啓発を実施しており、目的が昇進や配置転換・海外勤務といった会社主体に備えた理由の場合、重要度が著しく低くなる。企業規模や産業分類など、就業環境が職業設計に与える影響は限定的。また、「年齢階級」や「勤続年数」も総じて高くはなく、「最終学歴」や「業務」内容といった就業内容の重要度が高い。
(決定木分類の分析結果について(補足))決定木による分類は、分割を重ねれば重ねるほど予測誤差が小さくなる反面、データのノイズを拾いすぎて過学習が発生し分散が大きくなるという特徴がある。そこで、過剰に適合しない簡潔なツリーモデルを構築する必要があり、今回はその枝切にcp (複雑度:complexity parameter)を用いた。本稿における正社員のツリーモデルではcp=0.0052、正社員以外のツリーモデルはcp=0.0051である。
正社員の決定木は、ランダムフォレストの変数重要度で最大であった「最終学歴」より次点の「自己啓発の理由:将来の仕事やキャリアアップに備えて」が上位の分割変数となっている。これは説明変数の相互作用を考慮した上で、自分で職業設計をしたい人の比率がより特徴的・有意的に分割される説明変数が取捨された結果である1。
以下はランダムフォレストの変数重要度の高い順と同じである。「2:最終学歴」における「その他」は最終学歴が中学・高等学校・中等教育学校、専修学校・短大・高専及びその他が該当する。また、「3:役職」は係長・主任・職長相当職以上の役職が同じセグメントになったため「該当」と設定し、それ以外を「なし・不明」とした。
正社員以外の決定木においても、「自己啓発の実施」がランダムフォレストの変数重要度の順位を超えて最初の分割変数となった。これも説明変数間の相互作用を考慮した結果であり、変数重要度で高い値のある「性別」「雇用形態」で職業設計を自分で検討したい「男性」「契約社員」の多くが自己啓発を実施しているためである。また、「女性でパート」が多い影響もあり、より特徴を抽出する結果「性別」と「雇用形態」も変数重要度とは逆のツリー順になっている。
「5:業務内容」に関しては、業務の変数11種が以下のように分類された。これらのセグメントは、非常に大まかではあるが、工場や作業場等の現場作業が中心の業務とそれ以外で分類ができると考えられることから、本稿では「現業系」、「非現業系」と定義した。